2.1.2 Grundlagen der Wirtschaftlichkeitsrechnung für Investitionen


a) Warum Wirtschaftlichkeitsrechnung im Seetransport?
(Quelle: u.a. Buxton/Engineering Economics)

Neben der Sicherheit in der Schiffahrt (Schutz gegen Verlust von Gesundheit und Leben sowie gegen Beschädigung und Verlust von Schiff und Ladung) und dem Schutz der maritimen Umwelt stellt die Wirtschaftlichkeit des Seetransports ein sehr wichtiges gesellschaftliches wie auch individuelles Ziel dar.

Sparsamer Umgang mit dem knappen Wirtschaftsgut Kapital, Minimierung der Nutzung natürlicher Resourcen, Maximierung der Rendite und Minimierung des finanziellen Risikos sind u.a. Triebfedern für eine wirtschaftlich optimale Entwicklung des Seetransports. Insbesondere in einigen wesentlichen Segmenten des Seetransports, wo Überkapazitäten das Marktgleichgewicht erheblich stören, ist die Erzielung der wirtschaftlichsten Transportlösung ein Muss für das Überleben des Seetransportbetriebes.

In den letzten Jahrzehnten ist die Notwendigkeit wirtschaftlicher Optimierung des Seetransports zwar in das Bewusstsein der an Schiffahrt und Schiffbau Beteiligten eingedrungen, doch die Anwendung wirtschaftlicher Optimierung - insbesondere in der Kombination von Schiffbautechnik und Betriebswirtschaft - ist bisher noch nicht ausreichend vorangekommen, nicht zuletzt auch aufgrund der Tatsache, dass Reedereien (vielfach aus Unkenntnis technisch-wirtschaftlicher Zusammenhänge) und Werften (aus gleichen wie auch aus Konkurrenzgründen) das "billigste" Schiff anstreben, obwohl dieses oftmals nicht das "wirtschaftlichste" Schiff ist. Diesbezüglich ist also noch ein merkliches Umdenken und ein Ändern der Vorgehensweise notwendig, d.h. alle Entwurfsanstrengungen des Schiffbauers zur Senkung von Bau- und Betriebskosten des Schiffes müssen auch gleichzeitig durch betriebswirtschaftliche Untersuchungen begleitet werden.

Bis vor wenigen Jahrzehnten wurden recht einfache (sog. statische) Methoden ökonomischer Analysen angewandt (Kostenvergleichsrechnung, Gewinnvergleichsrechnung, Amortisationsrechnung etc.). Obwohl diese Methoden in unserer heutigen komplexen Wirtschaftssituation als ungeeignet zu bezeichnen sind, so bilden sie doch schon einen Schritt in die richtige Richtung. Diese einfachen Methoden beinhalten aber die Gefahr falscher Antworten, da sie entscheidende Faktoren ganz oder teilweise ausser Acht lassen, wie z.B.:
In den folgenden Abschnitten werden die Grundlagen für moderne (sog. dynamische) Wirtschaftlichkeitsrechnungen aufgezeigt und anhand kleiner Beispiele praktisch erläutert. Eine etwas ausführlichere Beispielrechnung für die optimale Lösung einer Seetranspotaufgabe folgt später.


b) Der Zinsfuss und abgeleitete Faktoren
(Quellen/weitere Info: Buxton/Engineering Economics and Ship Design; Benford/A Naval Architects Introduction To Engineering Economics; Scheffler/Prüfung von Investitionen)

i) Wesen und Funktion des Zinses:

Geld hat einen merklichen Zeitwert. 100 Euro heute zum Ausgeben zur Verfügung zu haben, ist von grösserem Nutzen als über 100 Euro in z.B. 10 Jahren zu verfügen. Wenn das Geld geliehen wird, muss eine Miete bzw. Belohnung, d.h. Zinsen, bezahlt werden, um dem Verleiher für das Verschieben der eigenen bzw. anderweitigen Nutzung zu entschädigen. Der Begriff des Zinses ist aber nicht nur als Belohnung für das Ausleihen von Geld (z.B. der nominelle Zins auf einen Bankkredit) zu verstehen, sondern ist fundamental für alle ökonomischen Berechnungen. So ist unter Zins auch eine Verzinsungsrate zu verstehen, die durch den Überhang der Einnahmen über die Ausgaben erzeugt wird.

In der dynamischen Wirtschaftlichkeitsrechnung hat der Zins auch folgende Funktion:
Die mit der Investition verbundenen Einnahmen und Ausgaben fallen zu verschiedenen Zeitpunkten an. Der Zins - volkswirtschaftlich als Preis für das knappe Wirtschaftsgut Kapital definiert - drückt den wirtschaftlichen Tatbestand aus, dass eine zeitlich frühere Einnahme mehr Wert ist, als eine spätere Einnahme. Andererseits bedeutet eine später fällige Ausgabe wirtschaftlich eine geringere Belastung als eine frühere Ausgabe.
Der Zins und der Zeitpunkt der Einnahmen und Ausgaben bestimmen deren wirtschaftlichen Wert. Die in die Rechnung einzubeziehenden Zahlungen sind daher durch Auf- oder Abzinsen auf einen einheitlichen Zeitpunkt zu beziehen (Bezugszeitpunkt). Eine Zahlung (Einnahme oder Ausgabe) im Zeitpunkt Null (Gegenwart) hat die gleiche wirtschaftliche Wertigkeit wie die um die Zinsen für die Zeit von Null bis zum Zeitpunkt t erhöhte Zahlung im Zeitpunkt t.
Die Summe der zum Kalkulationszinsfuss auf den Bezugszeitpunkt auf- oder abgezinsten Zahlungen, die mit der Investition verbunden sind, bezeichnet man als Kapitalwert der Investition.
Üblicherweise werden für die Zeitreihen der Einnahmen und Ausgaben, die die Wirtschaftlichkeit der Investition bestimmen, deren Gegenwartswerte bestimmt, die miteinander vergleichbar sind. sämtliche Zahlungen werden dementsprechend auf den Zeitpunkt Null abgezinst. Ebenso kann man auch mit den durch Aufzinsung erhältlichen Endwerten (Zeitpunkt t) der Zahlungsreihen rechnen. Wichtig ist nur die einheitliche Zeitbasis.

Den Investitionsrechnungen können entweder jährliche Zahlungen (häufiges Verfahren) und damit ein Jahreszins zugrundegelegt werden oder aber auch kürzere Zahlungsperioden bzw. kontinuierliche Zahlungen mit entsprechenden Zinssätzen.

ii) Nomenklatur:

In den nachfolgenden Formeln gilt folgende (vornehmlich amerikanische) Nomenklatur:


iii) Auf- bzw. Abzinsung von Einzelbeträgen:

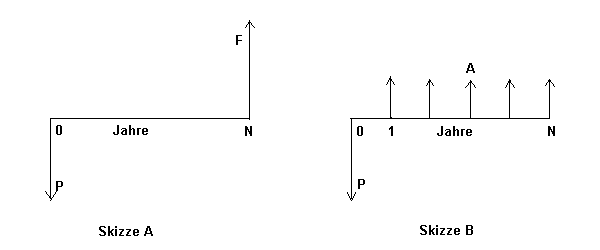
Die nachfolgende Skizze A stellt die Beziehungen zwischen einem Einzelbetrag zum Zeitpunkt Null und N Jahre in der Zukunft dar.

In dieser Skizze ist:

F = CA * P

Der darin enthaltene Aufzinsungsfaktor CA hat folgende algebraische Beziehung (bekannt auch als Zinseszins):

CA = (1 + i)N

Andererseits ist:

P = PW * F

Der darin enthaltene Abzinsungsfaktor PW ist der Reziprokwert von CA mit folgender algebraischer Beziehung:

PW = 1 / CA = 1 / (1+i)N

Dazu ein numerisches Beispiel:

Ermittle den Gegenwartswert einer in 15 Jahren erwarteten Zahlung in Höhe von 1000 Euro bei Anwendung eines Kalkulationszinsfusses von 8%:

P = PW * F = 0,315 * 1000 = 315 Euro




iv) Behandlung von regelmässigen und gleich grossen Beträgen:

In vielen Wirtschaftlichkeitsuntersuchungen werden gleich grosse jährliche Zahlungen (Einnahmen bzw. Ausgaben bzw. Einnahmen-Ausgaben-Differenzen) angenommen, obwohl bekannt ist, dass meistens keine Gleichförmigkeit auftritt. Man ist jedoch oftmals nicht in der Lage, die Schwankungen in den jährlichen Zahlungen mit ausreichender Genauigkeit vorauszusagen. Aus dieser Annahme resultierende Fehler können aber in vielen Fällen von Alternativvergleichen akzeptiert werden, da sie jeweils prozentual gleich gross angenommen werden können. Wenn wir gleichzeitig annehmen, dass der Investitionsbetrag in einer Summe am Tag vor Betriebsbeginn der Anlage (bzw. des Schiffes) bezahlt wird, dann ergibt sich ein "Cash-Flow"-Muster wie es in der obigen Skizze B dargestellt ist.

Wenn wir die in dieser Skizze B dargestellten gleich grossen jährlichen Zahlungen A kennen und den Gegenwartswert P dieser Zahlungsreihe suchen, benutzen wir den Serien-Abzinsungsfaktor SPW, d.h.:

P = SPW * A

Die algebraische Beziehung für den SPW lautet:

SPW = (1 + i)N - 1 / i * (1 + i)N

Wenn wir andererseits die Höhe des Investitionsbetrages P kennen und die entsprechende jährliche Zahlung A wissen wollen, benutzen wir den Wiedergewinnungsfaktor CR, der der Reziprokwert des SPW ist:

A = CR * P

Die algebraische Beziehung für den CR lautet:

CR = 1 / SPW = i * (1 + i)N / (1 + i)N - 1

Numerisches Beispiel für die Anwendung des SPW:

Ermittle den Gegenwartswert einer Reihe von gleich grossen jährlichen Zahlungen in Höhe von 1000 Euro, die über N = 5 Jahre zu leisten sind, bei Anwendung eines Kalkulationszinsfusses i = 8%:

P = SPW * A = 3,993 * 1000 = 3993 Euro.

Man kann natürlich auch (aufwendiger!) die einzelnen jährlichen Beträge nach der Formel P = PW * F abzinsen und summieren, um das gleiche Ergebnis zu erhalten:

N
A
PW
P
1
1000
0,926
926
2
1000
0,857
857
3
1000
0,794
794
4
1000
0,735
735
5
1000
0,681
681
Summe
3993


Weitere Faktoren für weniger gebräuchliche Wirtschaftlichkeitsuntersuchungen siehe Hinweis unter der obigen Überschrift "b) Der Zinsfuss und abgeleitete Faktoren"

v) Die Wahl des Kalkulationszinsfusses:

Sehr umstritten ist die Höhe des anzusetzenden Kakulationszinsfusses i. Die Wahl ist deswegen problematisch, da sie sehr wesentlich das Ergebnis einer Wirtschaftlichkeitsrechnung beeinflussen Kann. Bei hoher Abzinsung werden die später liegenden Zahlungen geringer bewertet als bei niedrigerem Zinsfuss. Für die Beurteilungsfähigkeit des Ergebnisses ist daher die Objektivität des gewählten Zinsfusses erforderlich. Nach "Scheffler/Prüfung von Investitionen" kann man den landesüblichen Zins (z.B. für Wertpapiere) als objektiven Massstab ansetzen, da auch die Anlage des Kapitals in Finanzvermögen eine Investitionsalternative für den Unternehmer darstellt.

Besondere Risiken einer Investition sollten nicht durch Erhöhung des Zinsfusses abgedeckt sondern bei der Bewertung des Einnahmeüberschusses berücksichtigt werden. Ebenso sollten Inflationszuschläge bei den Ausgaben Berücksichtigung finden.


c) Verfahren der dynamischen Investitionsrechnung

i) Die Kapitalwertmethode:

Soll mit einer Investition "Gewinn" erzielt werden - und diese Absicht wird als Unternehmensziel unterstellt - so müssen die mit der Investition verbundenen Ausgaben unter Berücksichtigung des Zeitfaktors durch die Einnahmen mehr als wiedergewonnen werden. Das bedeutet, dass die auf einen einheitlichen Zeitpunkt auf- bzw. abgezinsten Einnahmen grösser als die ebenso auf- oder abgezinsten Ausgaben sein müssen.

Die Differenz zwischen den Gegenwartswerten der Einnahmen (auf den Zeitpunkt Null abgezinste Einnahmen) und der Ausgaben (auf den Zeitpunkt Null abgezinste Ausgaben) stellt den Kapitalwert der Investition NPV (Net Present Value) dar. Eine Investition ist bei einem gegebenen Kalkulationszinsfuss demnach dann vorteilhaft, wenn ihr Kapitalwert positiv ist. Bei der Kapitalwertmethode wird also das Vorzeichen des errechneten Kapitalwertes als Beurteilungsmassstab verwendet. Bei Vergleich von Investitionsalternativen ist darüberhinaus die Höhe des Kapitalwertes entscheidend; die Alternative mit dem höheren (positiven) Kapitalwert ist die wirtschaftlichere.

Kleines Beispiel:
- Anschaffungsausgabe P = 200.000,- Euro
- Restwert (Schrotterlös) R = 20.000,- Euro
- Nutzungsdauer N = 5 Jahre
- Kalkulationszinsfuss i = 8%
- jährliche Einnahmen a = siehe Tabelle
- jährliche Ausgaben b = siehe tabelle

N
a
b
a - b
PW
P
0
0
200.000
-200.000
1,000
-200.000
1
80.000
40.000
40.000
0,926
37.040
2
100.000
40.000
60.000
0,857
51.420
3
100.000
50.000
50.000
0,794
39.700
4
100.000
50.000
50.000
0,735
36.750
5
100.000
60.000
40.000
0,681
27.240
5
20.000
0
20.000
0,681
13.620
500.000
440.000
60.000
NPV =
5.770


Die Investition hat also einen positiven Kapitalwert und ist demnach vorteilhaft. Würde man jedoch den Restwert in Höhe von 20.000,- Euro nicht erwarten können, wäre der Kapitalwert 5.770,- minus 13.620,- = -7.850,- Euro. Diese Investition ist nicht "gewinnbringend", da der Kapitalwert negativ ist.


Ein schiffsbezogenes detailliertes Beispiel folgt in Abschnitt 2.1.3.


ii) Die "Interne Zinsfuss"-Methode:

Bei der "internen Zinsfuss"-Methode (Yield oder Discounted Cash Flow Rate of return) wird der "interne Zinsfuss" der Investition mit dem Kalkulationszinsfuss verglichen, der die vom Investor gewünschte (Mindest-)Rentabilität ausdrückt. Die Investition ist dann vorteilhaft, wenn ihr "interner Zinsfuss" grösser ist als der Kalkulationszinsfuss.

Der "interne Zinsfuss" ist derjenige Diskontierungszinsfuss, bei dem die auf einen gemeinsamen Zeitpunkt bezogenen Einnahmen und Ausgaben einen Kapitalwert NPV von Null ergeben.

Die "interne Zinsfuss"-Methode liefert ein recht anschauliches Ergebnis über die Vorteilhaftigkeit einer Investition. Bei unregelmässigen und/oder nicht gleich grossen Einnahmen und Ausgaben ist die Ermittlung des "internen Zinsfusses" aber recht schwierig und nur über eine iterative Prozedur zur Erreichung eines Null-Kapitalwertes zu lösen.

Bei gleich grossen jährlichen Zahlungen, d.h. bei einer gleichmässigen Zahlungsreihe, kann man den "internen Zinsfuss" über den Wiedergewinnungsfaktor CR ermitteln:

CR = A / P

Der "interne Zinsfuss" i wird dann als Funktion der Nutzungsdauer N und dem (ggfls. zu interpolierenden) Tabellenwert CR einer mittels der Formel CR = i*(1+i)N / (1+i)N-1 erstellten Tabelle entnommen.

Kleines Beispiel:

Regelmässiger jährlicher Einnahmeüberschuss A = a - b = 30.000 Euro
Anschaffungsausgabe P = 100.000 Euro
Nutzungsdauer N = 4 Jahre

CR = 30.000 / 100.000 = 0,3; i nach Tabelle = 7,7%

Dieser Zinsfuss kann als vorteilhaft bezeichnet werden, wenn i gleich oder grösser ist als die vom Unternehmer erwartete Mindestrentabilität der Investition.


iii) Die Annuitätsmethode:

Bei der Annuitätsmethode werden die mit der Investition verbundenen Reihen der in den einzelnen Zeitpunkten in unterschiedlicher Höhe anfallenden Einnahmen und Ausgaben in äquivalente Reihen mit gleich grossen Zahlungsbeträgen umgeformt, indem die Gegenwartswerte der effektiven Zahlungen mit dem Wiedergewinnungsfaktor CR multipliziert werden.
Die so gewonnenen gleich grossen Zahlungen je Periode (Annuitäten) stellen die unter Berücksichtigung des Zinsfaktors durchschnittlichen periodischen Einnahmen und Ausgaben dar. Eine Investition ist dann vorteilhaft, wenn die durchschnittlichen Einnahmen der Rechnungsperiode nicht kleiner sind als die durchschnittlichen Ausgaben der Periode.

Bei Schiffswirtschaftlichkeitsuntersuchungen - insbesondere bei Vergleich von Alternativen - wird ein Spezialfall der Annuitätsmethode angewandt. Hierbei geht man von der Anschaffungssumme P, deren Wiedergewinnung durch Multiplikation mit dem Wiedergewinnungsfaktor CR auf die einzelnen Perioden verteilt wird, sowie von gleich grossen Betriebskosten AOC (Annual Operating Cost) je Zahlungsperiode aus. Die Einnahmen werden im Berechnungsvorgang dabei ausser Acht gelassen. Man ermittelt also nur die durchschnittlichen Ausgaben je Zahlungsperiode.
In der Praxis sieht das so aus, dass man z.B. die jährlichen Gesamtkosten AAC (Average Annual Cost, in der Investitionsrechnung für Schiffe als Ersatz für die jährlichen Ausgaben b gewählt) verschiedener Alternativen mit gleich(!) grosser Transportleistung oder aber die jährlichen Gesamtkosten AAC, geteilt durch die Jahrestransportleistung C, vergleicht.
AAC geteilt durch C ergibt die sog. Mindestfrachtrate RFR (Required Freight Rate) pro Tonne Ladung. Die Alternative mit den geringsten AAC bzw. der kleinsten RFR ist die vorteilhafteste.

Formelmässig sieht das so aus:

AAC = CR * P + AOC

bzw.

RFR = AAC / C = CR * P + AOC / C

Sofern auch der Restwert R der Investition (z.B. Schrotterlös) berücksichtigt werden Kann/soll, sind die jährlichen Gesamtkosten wie folgt zu ermitteln:

AAC = CR * P + AOC - CR * R * PW.

Kleines Beispiel:
- Anschaffungskosten P = 60.000 Euro
- jährliche Betriebskosten AOC = 4.000 Euro
- Nutzungsdauer N = 6 Jahre
- Restwert R = 5.000 Euro
- Kalkulationszinsfuss i = 8% p.a.

- CR errechnet zu 0,216
- PW errechnet zu 0,630

AAC = 0,216 * 60.000 + 4.000 - 0,216 * 5.000 * 0,630 = 16.279,60

Die Anschaffung ist dann vorteilhaft, wenn mit ihr durchschnittliche jährliche Einnahmen (unter Berücksichtigung der Abzinsung) von 16.279,60 Euro und mehr erzielt werden bzw. Alternativen gleicher Leistungsfähigkeit ein höheres AAC ergeben.


vi) Wahl des Verfahrens:

Wie z.T. schon oben erwähnt, liefert die "interne Zinsfuss"-Methode zwar ein anschauliches Ergebnis, ist aber bei der komplexen Berechnung der Schiffswirtschaftlichkeit zu schwierig und daher ungeeignet.
Für den Vergleich von Alternativen wird in der Schiffswirtschaftlichkeit vornehmlich die
Annuitätenmethode verwendet. Da sie aber von merklichen Vereinfachungen ausgeht und die Einnahmenseite vernachlässigt, sollte für die endgültige Entscheidung, ob die günstigste Alternative auch wirklich gewinnbringend ist, eine detaillierte Ermittlung des Kapitalwertes nach der Kapitalwertmethode für diese Alternative durchgeführt werden.


d) Weitere Aspekte bei Wirtschaftlichkeitsuntersuchungen:

Bei den vorstehend beschriebenen Verfahren bzw. den ergänzenden kleinen Beispielen wurden nur die grundlegenden Bestandteile einer Wirtschaftlichkeitsrechnung angesprochen. Bei detaillierten Untersuchungen (siehe Berechnung nach der Kapitalwertmethode im nächsten Abschnitt) sind u.a. folgende weitere Aspekte zu berücksichtigen:

i) Kredite (Credits, Loans):

Üblicherweise werden die Baupreise von Schiffen nur zum geringeren Teil aus Eigenmitteln des Reeders bezahlt (min. 20%, vielfach wird heute von Banken schon 40 bis 50% verlangt). Der weitaus grösste Teil wird durch (Bank-)Kredite finanziert.
Bei den Einnahmen und Ausgaben einer Wirtschaftlichkeitsrechnung sind neben den Eigenmitteln die Auszahlungen des Kredits sowie die Rückzahlungsraten entsprechend den zu erfragenden Kreditmodalitäten (Zeitpunkte und Höhe der Auszahlungsraten, evtl. Tilgungsfreijahre, Zeitpunkte und Höhe der Tilgung und Zinsen) auf- bzw. abgezinst zu berücksichtigen.
Ebenso sind Bankgebühren in Verbindung mit der Kreditgewährung in der Wirtschaftlichkeitsrechnung einzubeziehen.
Der Kapitaldienst (Zinsen und Tilgung) erfolgt im Schiffskreditgeschäft üblicherweise so, dass die Tilgung in gleich grossen halb- oder vierteljährigen Raten erfolgt, während die Zinsen real, d.h. abfallend, in gleicher Frequenz bezahlt werden (klassische Form des Kapitaldienstes im Schiffskreditgeschäft). Im Gegenteil dazu wird der Kapitaldienst bei einem Immobilienkredit meistens in gleich grossen Raten (sog. Annuitäten) zurückgezahlt, d.h. abfallende Zinsen und adequat steigende Tilgung.
Durch die zunehmende Internationalisierung bzw. Europäisierung der Finanzmärkte geht aber auch der Kapitaldienst im Schiffskreditgeschäft mehr hin zur teilweisen Rückzahlung in Annuitäten. Diese Internationalisierung bzw. Europäisierung hat auch dazu geführt, dass der klassische Festzinskredit z.T. abgelöst wird durch Kredite mit variabler Zinsanpassung unter Abdeckung der damit verbundenen Zins- und Währungsrisiken (siehe hierzu HANSA 1995, Nr.3, S.8ff).

ii) Preis- bzw. Kostensteigerungen (Escalation):

Seit Jahrzehnten steigen die Preise fast aller Güter und Dienstleistungen aufgrund Geldwertverlust und Kostensteigerungen und zwar je nach jeweiliger Marktlage in unterschiedlicher Höhe. In einer detaillierten Wirtschaftlichkeitsrechnung muss dieser Tatsache bei der Festlegung der jährlichen Ausgaben im Einzelnen Rechnung getragen werden. Bei den Einnahmen ist diesbezüglich natürlich die zukünftige Marktentwicklung zu beachten. So sind oftmals Charterverträge nur mit gleichbleibenden Raten abschliessbar, d.h. ohne Ausgleich für schleichende Inflation etc..

iii) Subventionen (Subsidies):

Viele Schiffbaunationen gewähren ihren Werften zur Bestandssicherung bzw. zur Steigerung des Marktanteils direkte Baukostensubventionen (und oftmals auch indirekte Subventionen wie z.B. Zinssubventionen für Anlagenkredite) in unterschiedlicher Höhe. Direkte Baukostensubventionen sind bei der Schiffspreiskalkulation in Abzug zu bringen.
Darüberhinaus werden eigenen Reedern, aber auch Reedereien z.B. aus Entwicklungsländern, Zinssubventionen auf Baukredite (zinsvergünstigte Kredite) gewährt, sowie z.B. deutschen Reedern bzw. deren Anteilseignern Sonderabschreibungen und Verlustzuweisungen ermöglicht.
Damit die daraus resultierende internationale Marktverzerrung reduziert (besser: eliminiert) wird, wurden internationale Abkommen im Rahmen der OECD getroffen bzw. verhandelt (siehe hierzu Kapitel 1). Die jeweils erreichbaren Subventionen sind in der Wirtschaftlichkeitsrechnung angemessen zu berücksichtigen.

iv) Steuern (Taxes):

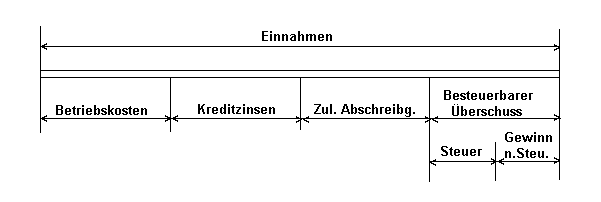
Einnahmeüberschüsse werden üblicherweise durch Unternehmenssteuern reduziert und zwar prozentual auf diese Überschüsse bezogen.
Die zu besteuernden Einnahmeüberschüsse (Gewinne) ergeben sich ganz generell aus Einnahmen minus Betriebskosten minus Kreditzinsen minus zulässigen Abschreibungen (linear oder degressiv). Die daraus resultierenden Steuern sind bei der Ermittlung der Kapitalwerte in Abzug zu bringen. Grafische Darstellung der Besteuerung:


Hinsichtlich Steuervorteile für die deutsche Seeschiffahrt siehe z.B. HANSA 1994, Nr.10, S.16ff, wobei jedoch zwischenzeitliche Novellierungen zu beachten sind.


zurück zum Inhaltsverzeichnis